Tormek Square-Edge Jig Protrusion Calculator
This tool can be used to calculate the amount of protrusion needed to get a given bevel angle using the Tormek square-edge jig (SE-77). Setting up the Tormek with the angle setter is quite time consuming (compared to using a simple reference with a honing guide). By fixing the offset from the support bar to the wheel, a fixed tool protrusion can be used, which speeds up the setting process, especially if you have one of these edge distance gauges.
This calculator can either work out bevel angle (if you're finishing the edge with a bench stone) or tip angle (if you're using the edge produced by the Tormek directly). The difference between these angles is explained below.
It's worth noting that the protrusion for a given bevel angle (but not tip angle) will also vary with tool thickness (as it will with a plane blade fitted into an Eclipse style honing jig) and also with wheel diameter. The effect of tool thickness is probably small enough to be ignored and wheel diameter will change fairly gradually (or not at all if you're using a diamond wheel), so I don't see this as too big an issue.
| Wheel Diameter (mm): | mm | |
| Distance from Support bar to Wheel Edge† (mm): | mm | |
| Support Bar Setting Tool Diameter‡ (mm): | mm | |
| Tool Thickness (mm): | mm | |
| Bevel Angle (°): | ° | |
| Tip Angle (°): | ° | |
| Tool Protrusion (mm): | mm |
The following parameters probably won't need to be adjusted unless you're not using the SE-77 square-edge jig (or your SE-77 is a different size to mine for some reason). These parameters are described later in the page.
| Reference Face Offset (mm): | mm | |
| Protrusion Offset (mm): | mm |
Footnotes
† Useful gaps for reference:
- DBS-22 Set-up gap: 14 mm (setting tool diameter 40 mm)
- TTS-100 Hole A Set-up gap with 250 mm diameter wheel: 51 mm (setting tool diameter 112 mm)
- TTS-100 Hole B Set-up gap with 250 mm diameter wheel: 22 mm (setting tool diameter 56 mm)
- TTS-100 Hole A Set-up gap with 200 mm diameter wheel: 56 mm (setting tool diameter 124 mm)
- TTS-100 Hole B Set-up gap with 200 mm diameter wheel: 30 mm (setting tool diameter 72 mm)
‡ The setting tool referred to here is a simple tool that speeds up the process of setting up the support bar. The idea was invented by Micha Schmid and Keld Petersen on the Tormek forum. It is simply a cylindrical piece of aluminium (or similar) with a 12 mm hole drilled through the centre. A flat is added on one side to aid removal (by rotating the grinding wheel until the flat is over the wheel, which removes the contact between the wheel and the setting tool and makes it easy to slide the setting tool off).

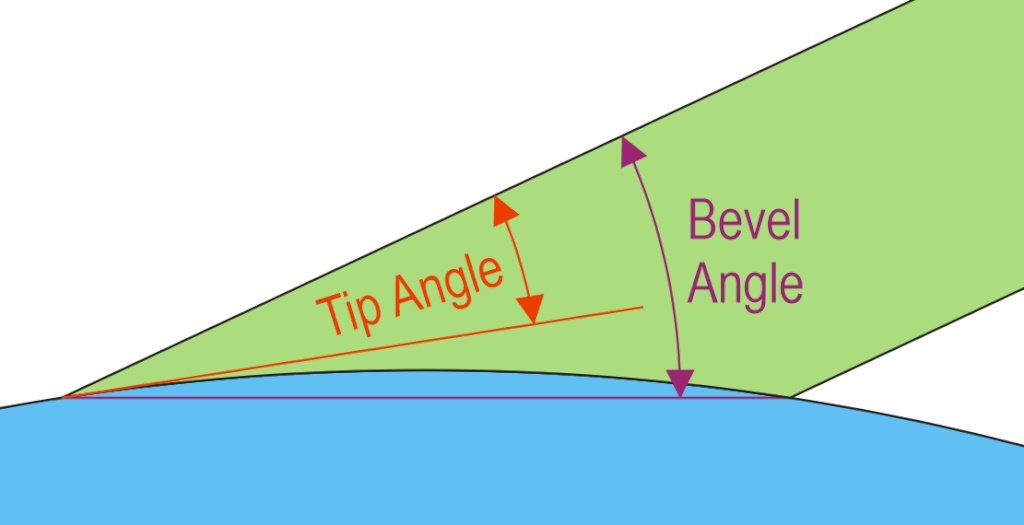
Bevel Angle vs Tip Angle
Here, the bevel angle is defined as the angle between the flat back of the tool and the line that joins the tip to the rear of the bevel. The tip angle is defined as the angle right at the very tip. These are shown graphically here with the red line tangent to the grinding wheel (in the diagram, the effect of the wheel radius is greatly exaggerated):
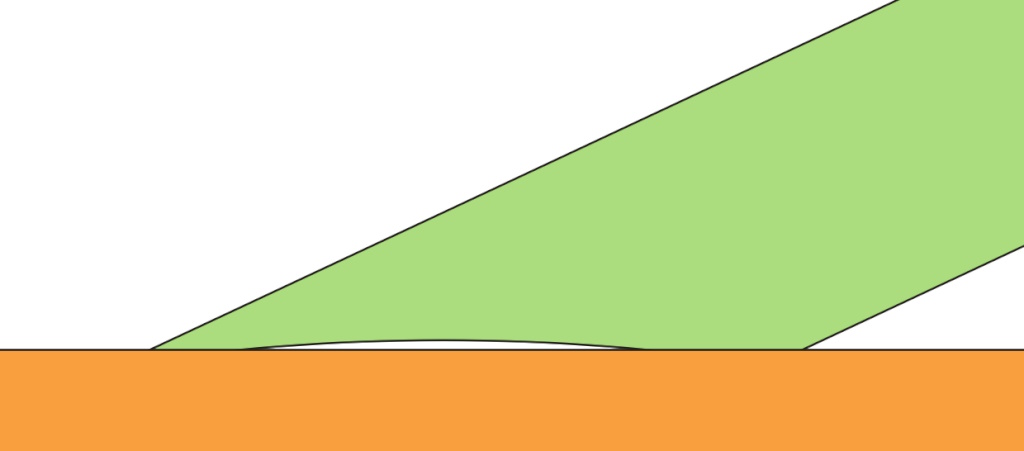
If, like me, you like to finish (and/or resharpen) your edges on a fine bench stone, working to a particular bevel angle is beneficial. When you then move over to the bench stones you can match that angle by resting the two extremes of the bevel on the stone and then grinding the outer extremes of the bevel, as shown here:
Alternatively, you can match or slightly increase the angle when using a honing guide (see my honing guide calculator) and be sure you'll only be hand-grinding the very tip.
If, however, you prefer to use the tool straight off the Tormek, then the cutting angle will be the tip angle and if you're targeting a particular angle then you should use the tip angle field in this calculator. Unlike the bevel angle, the tip angle is not dependent on tool thickness.
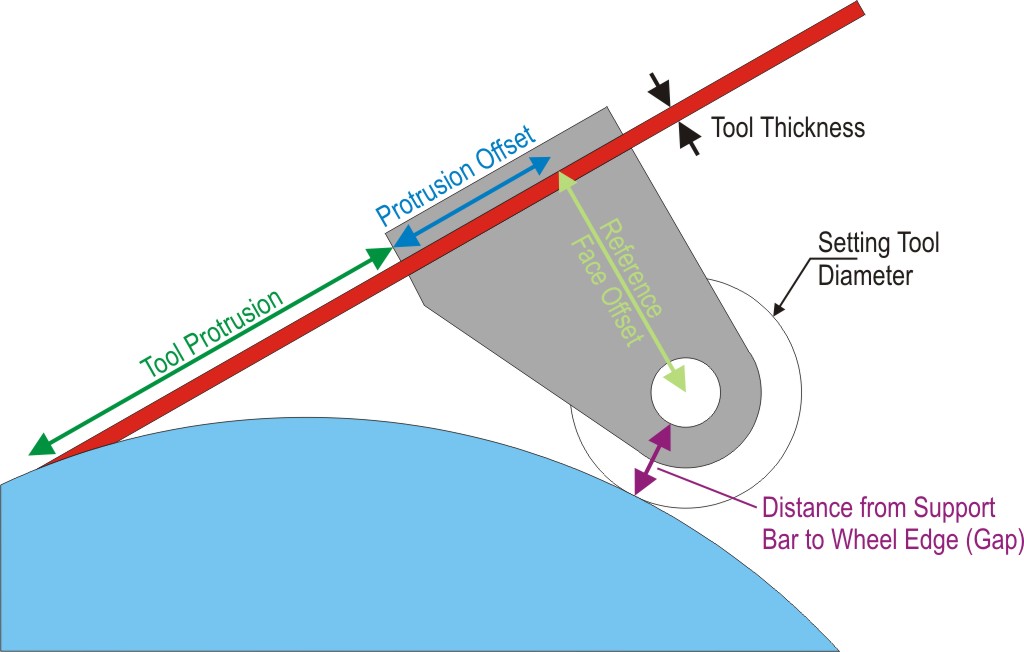
Offsets
The reference face offset in the table above is the distance from the centre of the support bar to the face of the jig against which the tool is clamped. The protrusion offset is slightly more complicated to describe. If you draw a line from the centre of the support bar to the face of the jig against which the tool is clamped and ensure that line is perpendicular to the face, it is the distance from the point where that line meets the clamp face to the edge of the jig from which you measure the protrusion. Both of these dimensions are shown graphically in the diagram below:
Background
This calculator uses the following equations:
Key
\(\qquad g\) is the distance from the grinding wheel to the centre of the support bar.
\(\qquad \qquad\) (i.e. the distance from support bar to wheel edge plus the radius of the support bar (6 mm)
\(\qquad r\) is the radius of the grinding wheel (wheel diameter divided by 2).
\(\qquad t\) is the tool thickness.
\(\qquad s\) is the reference face offset.
\(\qquad l\) is the tool protrusion plus the protrusion offset.
\(\qquad \theta\) is the bevel angle.
\(\qquad \alpha\) is the tip angle.
All other variables (\(u, \phi, k\)) are intermediate values used to simplify the maths.
Calculations
Calculating protrusion from bevel angle:
$$ u = \frac{t}{\tan(\theta)} $$ $$ \phi = 2 \tan^{-1}\left(\frac{2 r t \pm \sqrt{-(t^2 + u^2)(t^2 + u^2 - 4 r^2)}}{t^2 + u^2 - 2 r u} \right) $$ where \(\phi \gt 0\). $$ l = - r \cos(\phi) \pm \sqrt{g^2 + 2 g r + r^2 \cos^2\phi + 2 r s \sin\phi - s^2} $$ where \(l \gt 0\).
Protrusion is then \(l\) minus the protrusion offset.
Calculating bevel angle from protrusion:
$$ k = \frac{g^2 + 2 g r - (l^2 + s^2)}{2 r} $$ $$ \phi = \frac{\pi}{2} - \left( \sin^{-1}\left(\frac{k}{\sqrt{l^2+s^2}}\right) + \tan^{-1}\left(\frac{s}{l}\right)\right) $$ $$ u = \sqrt{r^2 \cos^2\phi + 2 r t \sin\phi - t^2} - r \cos\phi $$ $$ \theta = tan^{-1}\left(\frac{t}{u}\right) $$
Thanks to John Alexiou for his help with this calculation.
Calculating \(\phi\) from tip angle or vice versa:
$$ \phi = 90 - \alpha $$ From there, the bevel angle or protrusion can easily be calculated as above. To go back the other way is obviously: $$ \alpha = 90 - \phi $$
This website is free and ad-free, but costs me money to run. If you'd like to support this site, please consider making a small donation or sending me a message to let me know what you liked or found useful.